Symmetric Cryptrography
encrypt 와 decrypt 에 같은 key 를 사용한다.
따라서 n명의 사람들이 communicate 하려면,
총 key 의 개수는 n(n-1)/2 로 n^2 에 가까운 많은 key 가 필요하게 된다.
Asymmetric Cryptography
encrypt 할 때에는 public key로, decrypt 할 때엔 private key 를 사용한다.
이때는 n명의 사람이 있다면 2n 개의 key 만 존재하므로,
key 관리가 매우 쉬워진다.
public key
누구에게나 공개된다.
encrypt 하는데 사용된다.
verify signature
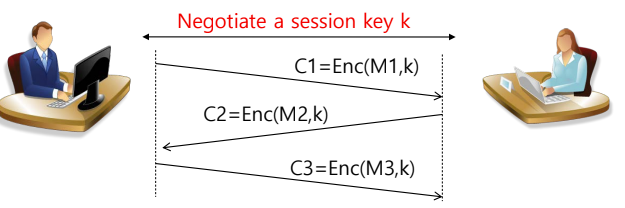
key exchange (session keys)
private key
recipent 만 가지고 있다.
decrypt 하는데 사용된다.
sign(create) signature
-> public key(encryption key)와 algorithm 만으로 decryption key 를 찾는 것은 어렵다.
Security of Public Key Algorithms
key 는 충분히 크다. -> 512bits, 1024bits...
known hard problem
대칭 key schemes 에 비하면 매우 느리다
Known Hard Problem : "Trapdoor Functions"
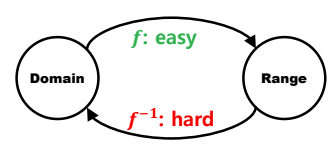
domain->range 는 쉽지만, range->domain 은 어렵다.
ex) Prime Factorization : p,q 라는 아주 큰 소수가 있을 때, z=pq 를 계산하는 것은 쉽지만,
z에서 p와 q 를 추출하는 것은 어렵다. -> RSA, Paillier
ex) Discrete Logarithm Problem : 두 정수 g,x가 존재할 때 a=g^x mod p 를 계산하는 것은 쉽지만,
g,a가 주어질 때 x를 계산하는 것은 어렵다. -> Deffie-Hellman, Digital Signature, Elliptic Curve
ect -> Kanpsack, Matric Permuation ...
RSA
-Mathematic Background of RSA
-RSA cryptosystem
-RSA digital signature
-RSA cryptanalysis
Fermat's Theorem

Euler's Theorem
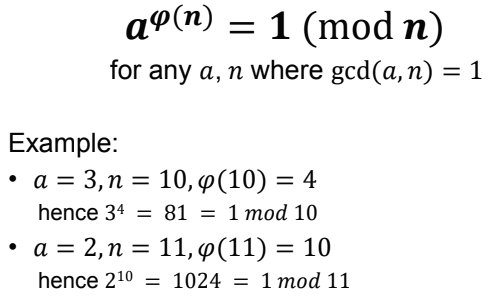
Testing for Primality
RSA과 같은 cryptographic 알고리즘에서는 랜덤의 아주 큰 소수를 선택하는 것이 매우 중요하다.
-> 무한한 소수가 존재한다. (Euclid 증명)

몇개의 소수가 존재하는가?
- Prime Number Theorem (PNT)
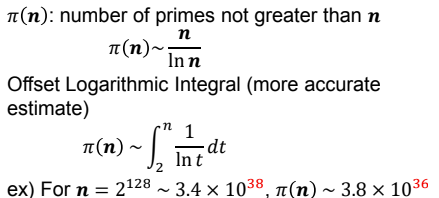
-> n = 128 bit 일 때, 3.8 x 10^36 개의 소수가 존재
- Naive Try

runnint time 이 O(n) 으로 그렇게 좋지 않다.
- Second Try

running time 은 O(√n) 으로 더 낫다.
-> n 이 합성수라면, n의 요소 중 가장 작은 소수는 √n 이하이다.

ex) 139 와 143 이 소수인지 테스트하자.
n 이 합성수라면 n의 요소 중 가장 작은 소수는 √n 이하일 것이다.
139 와 143 보다 큰 169 = 13^2 이므로, 13은 list 에 포함되지 않을 것이다.
따라서 prime list 를 {2,3,5,7,11} 로 정하고, 각 숫자를 나눠본다.
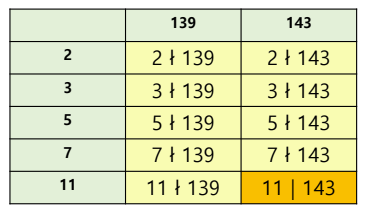
139 는 아무 소수로도 나눠지지 않고, 143은 11 * 13 으로 나눠지므로,
139 는 소수, 149 는 합성수 임을 알 수 있다.
Fermat's Little Theorem 으로 test 하기
p가 소수이고, a,p 가 서로소일 때 a^p-1 = 1 (mod p) 가 성립했다.
따라서 p가 소수라면 랜덤한 a를 선택했을 때 위 식이 성립할 것이다.
2 부터 n-1 까지 a를 랜덤하게 뽑고, 테스트했을 때 위 식이 성립하지 않는다면
p 는 합성수이고, 모두 성립한다면 아마 prime 일 것이다.

예시)

Miller-Rabin algorithm

홀수 n이 주어진다면, n-1 은 항상 짝수이므로 2^k*q 로 표현할 수 있다.


-> 이는 Fermat Little theroem 보다 훨씬 강한 판별법이다.

예시)

174^55 mod 221 = 47 로 1이 아니고, 220 도 아니다.
174^110 mod 221 = 220 으로 n-1 이 맞으므로 probably prime 일 수 있다.
a를 137 로 설정했을 때,
137^55 mod 221 = 88 로 1도 아니고, n-1 도 아니다.
137^110 mod 221 = 205 로 n-1 이 아니므로 221 은 합성수이다.
Integer Factorization Problem
아주 큰 p,q 소수가 주어졌을 때 N=pq 를 계산하는 것은 쉽지만,
N 이 주어졌을 때, N이 아주 크다면 p,q 를 찾는 것이 어렵다.
'정보보안' 카테고리의 다른 글
| 7. Public Key Cryptography - Diffie Hellman Key Exchange (0) | 2021.11.01 |
|---|---|
| 7. Public Key Cryptography - RSA (2) (0) | 2021.11.01 |
| 6. Basic Mathematics for Cryptography (0) | 2021.10.31 |
| 5. Conventional Cryptography Systems (0) | 2021.10.30 |
| 4. Theory of Secure Communication (0) | 2021.10.30 |



댓글