Constraint satisfaction problems (CSPs)

- 이전 챕터까지는 atomic representation 사용 -> 6장 부터는 Factored representation 사용 (state 를 표현하는 여러개의 variable 이 존재한다.)

- Constraint satisfaction problems (CSPs) : variable value 가 제약조건을 만족해야한다.

- CSP search 알고리즘은 general-purpose(범용) heuristic 이다. 반대로 이전까지 배운 search 알고리즘은 구체적인 문제의 heuristic 으로만 사용이 되었다.

 

 

Defining CSPs

- 세 가지 구성요소

• X : 변수 {X1, ... , Xn}
• D : 도메인 {D1, ... , Dn}
• C : 제약조건

- i 번째 제약조건인 Ci : <scope, rel> 의 쌍으로 구성된다.

• scope : 제약조건에 관련이 된 변수들
• rel : 변수들 사이에 지켜야할 relation(관계)

- 예)

-> 모든 제약조건은 관계로 나타낼 수 있다.

 

- CSP 의 state : 변수의 전부 또는 일부에 값이 할당된 상태 

• X1,X2 라는 변수가 있고, 도메인은 (A,B) 라면 X1 = A, X2 = A 와 같은 할당이 될 수 있다.

- 이런 state 중에서 제약조건을 위반하지 않는 state 를 consistent 또는 legal assignment 라고 한다.

- Complete assignment : 모든 변수가 값을 할당받은 상태

- CSP 의 solution (goal state) : Consistent(legal) 하면서 complete 한 assignment

 

 

 

Map Coloring

이웃 나라와 색이 겹치지 않게 모든 지도에 색을 칠하는 것

-> 9개의 나라간 경계가 존재하므로 9개의 제약조건이 필요하다.

 

 

 

Constraint Graph

- 특정 CSP 에 존재하는 제약을 graph 형식으로 표현한 것

- Vertex : 변수

- Edge : 제약

 

 

 

CSP 를 사용하는 이유

- CSPs 는 꽤 다양한 search 문제를 푸는데 사용될 수 있다.

- CSP solver 는 이전에 배웠던 많은 search 알고리즘보다 빠른 경우가 많다. -> 범용 heuristic 이 존재하므로

 

 

 

Variations on the CSP Formalism

- 가장 단순한 형태의 CSP 는 discrete variable(이산 변수)를 가지고, 유한한 domain 을 가지는 경우이다. -> 우리가 가장 많이 다루는 형태

- 이산 변수 이면서, 도메인의 크기가 무한한 경우가 있다.  

• 제약조건이 linear
• 제약조건이 non-linear

- 연속 변수

• linear programming, quadratic programming

- 제약조건 타입

• 단항, 이항, 삼항[Between(X,Y,Z)]... 
• CSP 를 구성하는 모든 변수에 대한 조건 Global constraint (Alldiff in Sudoku problem, cryptarithmetic puzzle)

 

 

A Cryptarithmetic Puzzle

알파벳 별로 들어갈 숫자를 찾는 문제이다.

 

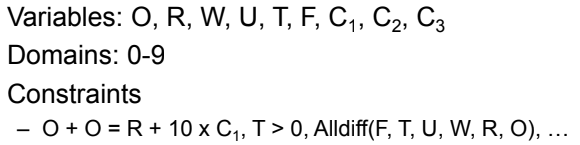
- 덧셈을 할 때 생기는 올림수(carry) 는 C1,C2,C3 으로 표현한다.

- 각 변수는 모두 다른 값을 가져야 한다. -> Alldiff

- 삼항 이상의 제약조건을 표현하기 위해서 Hyper edge (네모) 를 사용한다.