페르마의 소정리를 모르면 못 푸는 문제...
페르마의 소정리란 p가 소수이고, a가 p로 나누어지지 않는 정수 일 때 성립하는 법칙이다.
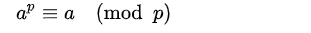
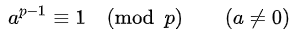
이 문제에서 정답을 구하기 위해선 결국 (n! / r! (n-r)!) 를 1234567891 로 나눈 나머지 값,
즉, (n! / r! (n-r)!) % 1234567891 을 구해야 한다.
결국 모듈러의 연산 공식을 활용해야 하는데, 모듈러 연산에서 나눗셈 연산은 허용되지 않는다!
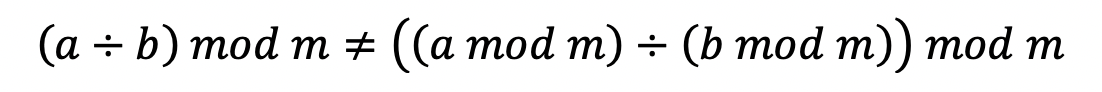
즉, r! (n-r)! 의 분모에 대한 모듈러 연산은 분배법칙을 적용할 수가 없음을 뜻한다.
따라서 모듈러 연산의 곱셈의 분배법칙을 이용해야 한다!!
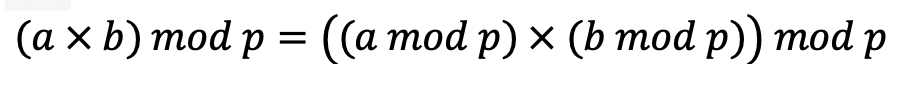
(n! / r! (n-r)!) 을 곱셈꼴로 만들기 위해선 역원을 이용해야 한다!

와 같다.
이때, 페르마의 소정리를 이용한다면 아래와 같다.
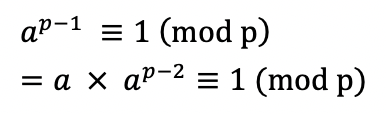
즉, a(mod p) 에 대한 역원은 a^p-2 (mod p) 임을 알 수 있다.
따라서 결국 우리가 구하고자 하는 값은 n! * ((n-r)!*(r!))^p-2 이다.
따라서 bottom = (n-r)!*(r!) 로 값을 구한 후, pow함수를 이용해 pow(bottom, p-2) 을 구하면 된다!!

나의풀이
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.StringTokenizer;
public class Solution {
static int T;
static long dp[];
static int n, r;
static final int P = 1234567891;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringBuilder sb = new StringBuilder();
StringTokenizer st;
T = Integer.parseInt(br.readLine());
dp = new long[1000001]; // dp[i] = i! % P
dp[1] = 1;
for (int i = 2; i <= 1000000; i++) {
dp[i] = (dp[i - 1] * i) % P;
}
for (int t = 1; t <= T; t++) {
st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
r = Integer.parseInt(st.nextToken());
// 분모
long bottom = (dp[n-r] * dp[r]) % P;
long B = pow(bottom, P-2);
long ans = (dp[n] * B) % P;
sb.append("# ").append(t).append(" ").append(ans).append("\n");
}
bw.write(sb.toString());
bw.flush();
bw.close();
}
static long pow(long a, int b) {
if (b == 0)
return 1;
else if (b == 1)
return a;
if (b % 2 == 0) { //
long tmp = pow(a, b / 2);
return (tmp * tmp) % P;
}
long tmp = pow(a, b - 1);
return (tmp * a) % P;
}
}'알고리즘 > 이것저것' 카테고리의 다른 글
| [백준] 1253번: 좋다 - java (0) | 2023.04.17 |
|---|---|
| [백준] 1493번: 박스 채우기 - java (1) | 2023.03.06 |
| [백준] 21939번: 문제 추천 시스템 Version 1 - java (0) | 2023.02.12 |
| [백준] 2023번: 신기한 소수 - java (0) | 2023.02.09 |
| [백준] 12891번: DNA 비밀번호 - java (0) | 2023.02.09 |



댓글