Informed Search
- 지금까지의 Uninforemd 와는 달리, 문제 정의 이외의 정보를 더 활용하여 효율적으로 검색을 하는 방법이다.
- Best-First Search : 트리 내 evaluation function f(n) 에 의해 cost가 가장 적은 노드를 판별하여 먼저 탐색한다.
- f(n) 은 heuristic function h(n) 을 포함하고 있다.
- h(n) 이란 n에서부터 goal 까지의 최소 비용을 예측하는 함수이다
- 예를 들어, Romania 문제에서 원래는 도시간의 비용이 지도에 주어졌지만, h(n)을 사용한다면 도시 n에서부터 goal 까지의 직선거리를 사용할 수 있다. (직선거리 = straight line distance -> SLD)
Greedy Best-First Search
- f(n) = h(n) 으로 오직 heuristic 한 추정치만을 사용하여 검색을 진행하는 방법이다.
- 즉, goal 에 가장 가까운 node를 expand 한다.
- Romania 문제에서 SLD 가 heuristic 을 결정한다.

- 위 사진은 각각의 도시에서 Bucharest 로 이르는 직선 거리를 보여준다.
- 위 정보는 문제에서 정의된 지식이 아닌, 추가적인 지식이다.
- SLD를 통해서 Tree-Based Search를 하면 다음과 같다.


- 검색 비용은 optimal 하지만, 결과는 optimal 하지 않음을 볼 수 있다.
-> (Sibiu -> Rimmicu -> Pitesti -> Burcharest) 가 optimal 한 solution이다.
Performance of Greedy Best-First Search
- Completeness
- Graph version : yes
- Tree version : No (DFS와 같음)
- Optimal : No
- Time and Space Complexity : O(b^m) , m은 트리구조에서 Search space 에서의 depth 의 최대값이다.
A* Search
- best-first search 로 가장 널리 알려진 알고리즘이다.
- f(n) = g(n) + h(n)
- 노드 n에 도달하기 위한 실제 비용 g(n) 과 노드 n 에서 goal 까지의 최소 비용을 예측한 추정 비용 h(n) 을 더한 값이다.
-> 노드 n을 거쳐서 goal 로 가는 경로 중에서 가장 비용이 저렴하다고 추정되는 비용의 추정치
- A* search 는 complete 하고, 최적의 경로를 알려주는데 적합하다.
- Uniform-cost-search 와 동일한 알고리즘이지만, priority queue 에 들어가는 가중치가 g(n) 이 아니라,
f(n) = g(n) + h(n) 이라는 것이 다르다.
- h(n) 이 특정한 조건들을 만족한다면, complete 하고 optimal 하다.
-> 최적화의 조건 : Admissibility, Consistency
Admissibility
- h(n) 이 Goal 까지 도달하는데 드는 비용을 절대로 과대평가 하지 않을 때 admissible 하다.
- 즉, 추정치 f(n) (= g(n) + h(n)) 는 절대로 실제 측정값보다 더 크게 추정해서는 안된다.
- 예를 들어, 서울에서 부산으로 가는 경로는 엄청 많으나 heuristic 함수인 서울-부산의 지도상 SLD 를 이용해서 최단경로를 검색한다고 했을 때, 서울-부산의 직선거리(heuristic 함수) 보다 짧은 실제 경로는 없을 것이기 때문이다. -> fn 이 실제 측정값보다 항상 크지 않은, 가장 작은 비용이다.
Consistency
- h(n) 이 h(n) <= c(n, a, n`) + h(n') 을 만족한다.
- 모든 n 노드와 자식노드(Successor) n′ 에 대해서, 노드 n에서 Goal에 도달하는 추정 비용은
노드 n에서 노드 n′ 까지 a라는 action 으로 가는 실제 비용과 노드 n′에서 Goal에 도달하는 추정 비용을 합한 것보다 작거나 같아야 한다.
- 이는 admissibility 보다 강력한 조건이다.
- Consistency 한다면 admissible 하다.
- Admissible 하더라도, Consistency 이지 않을 수 있다.
- Consistency → admissible (O)
- Admissible → Consistency (X)
- Consistency 가 Admissible 보다 더 강력한 조건임
- Consistent 하다면 항상 admissible함을 증명하기
- h(n) <= c(n,a1,n1) + h(n1) <= c(n,a1,n1) + c(n1,a2,n2) + h(n2) <= ... <= c(n,a1,n1) + c(n1,a2,n2) + ... + c(n_last,a_last,n_goal)
- 마지막에 c(n,a1,n1) + ... + c(n_last, a_last, n_goal) 은 h*(n) , 즉 goal 까지의 실제 경로가 될 것이다.
- 따라서 h(n) <= h*(n) 이므로 admissible 하다.
- Tree-search version : Admissible 하다면 Optimal 하다.
- Graph-search version : Consistent 하다면 Optimal 하다.
- Tree-search Romania Problem 예시
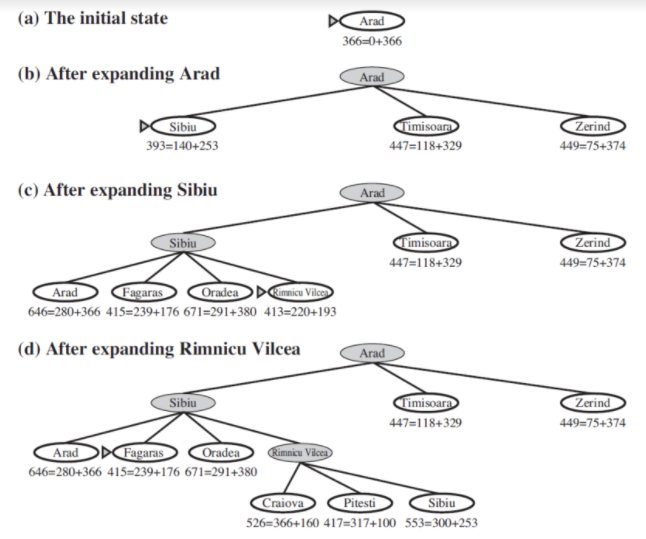
- (a) : root 부터 Arad 까지의 실제거리 0 + Arad에서 goal 까지의 직선 거리 366 = 366
- (b) : Arad를 expand 한 후, 자식들의 f(n) 을 계산하고 frontier 에 넣는다.
- (c) : Sibiu 확장 후, 자식들을 frontier 에 넣는다. 이때 Arad 가 중복해서 frontier 에 들어간다.
- (d) : frontier 에 있는 값들 중 가장 최소 비용인 Rimmicu 를 빼내고 expand 한 후 자식들을 frontier 에 넣는다.

- (e) : 다음으로 최소 비용인 Fagaras 를 expand 하고, 자식들을 frontier 에 넣는다.
- (f) : frontier 에 있는 것들 중 최소 비용인 Bucharest(418) 을 꺼내고, expand 한 후 goal 임을 확인하고 경로를 리턴한다.
Optimality of A*
- Tree-search version : Admissible 하다면 Optimal 하다.
- Graph-search version : Consistent 하다면 Optimal 하다.
- 위의 두 특성은 Uniform-cost Search 의 최적화에 대한 주장을 반영하는 특성이다.
- 만약 h(n) 이 consistent 하다면, 함수 f(n) 은 증가함수이다.
- n' 은 n의 successor (자식노드, 후임자) 이다.
f(n') = g(n') + h(n') = g(n) + c(n, a, n’) + h(n’) ≥ g(n) + h(n) = f(n)
-> f(n') >= f(n)
-> 따라서 f(n) <= f(n`) <= f(n``) <= …
- 즉, A* 가 다음 노드 n을 expand 했다면, n으로까지의 최적 경로를 이미 찾았다는 사실이 증명이 된다.
이는 모순에 의한 증명으로도 증명될 수 있다.
- 만약, 이것이 사실이 아니라면, 시작노드에서 n까지 가는 최적 경로상에 다른 frontier 노드 n' 이 있을 수 있다.
- 왜냐하면 f는 어떤 경로에 대해서도 항상 증가함수 이기 때문에, n' 은 n보다 낮은 f값을 가지고 있을 것이고 먼저 선택되었을 것이기 때문이다.
- 이는 f(n) >= f(n') 임을 뜻하고 모순이 발생했음을 알게 된다.
Contours by f(n) in a State Space
- A* 에 의해 expanded 된 node 들의 순서는 증가 함수인 f(n) 의 순서가 된다.

- f(n)의 등고선이 의미하는 바는 다음과 같다.
- A* search 가 수행될 때 작은 등고선 부터 차례로 탐색해나가는데, 해당 등고선 내부에 있는 노드들을 모두 탐색한 후에 다음 등고선으로 넘어가기 때문에 등고선이 뾰족하고 좁으면 더 적은 노드를 탐색한다는 것이다.
- 또한, hSLD 가 정확할 수록 적은 수의 노드를 expand 할 수 있다.
- Uniform-cost Search 는 (h(n)=0 이다) 등고선이 동심원을 그리게 된다.
- h(n) 이 0이라면 실제값인 g(n) 만으로 등고선이 그려지기 때문에 start state 에 가까울수록 0 에 가깝고, goal state 에 가까워질 수록 값이 커지게 되기 때문이다.
- c* 이 optimal cost 라면
- A* 는 모든 노드를 f(n) < C* 이 되도록 expand한다.
- A* 는 C* 보다 작거나 같은 f(n) 의 노드 수가 유한하다면 Complete 하다.
- A* 은 Optimal 알고리즘 중에 가장 빠르다.
- f(n) < C* 인 노드를 모두 탐색하기 때문에 Optimal 하다.
- f(n) < C* 이여도 탐색하지 않는다면 더 빠를 수는 있지만, Optimal 을 보장할 수 없다.
Computational Complexities of A* Search
- A* 탐색은 optimal, complete, 최상으로 효율적이다.
- 그러나, heuristic 의 오차가 발생할 수 있다. (h* 은 실제 비용)

- Time Complexity of A*

-> uninformed search 는 informed search보다 빠르기가 쉽지 않다.
- A* 의 Space complexity 는 시간 복잡도에 비해 매우 나쁘다. -> O(b^m)
'인공지능' 카테고리의 다른 글
| Admissible Heuristics from Subproblems, Pattern Databases (0) | 2021.10.18 |
|---|---|
| A* Search for N-puzzle Problem, Relaxed Problem (0) | 2021.10.18 |
| Iterative Deepening Depth-First Search, Bidirectional Search (0) | 2021.10.17 |
| Depth-First Search, Depth-Limited Search (0) | 2021.10.17 |
| Uniformed Search, BFS, UCS (0) | 2021.10.17 |



댓글