The 8-Puzzle Problem
- 8-퍼즐을 푸는데 평균적으로 22 step 이 걸리며, branching factor 은 평균 3이다.
- tree search 의 경우 3^22 개의 노드를 방문할 것이다 -> 3.1 x 10^10 node 에 달하는 큰 수
- graph search 의 경우 1700000개의 노드를 방문할 것이며, 15-puzzle 의 경우 10^13 에 달할 것이다
A* Serach for the n-Puzzle Problem
- 두 개의 Admissible heuristics 을 사용할 수 있다.
- 즉, 절대 goal 까지 가는데 걸리는 step 을 넘지 않는 heuristic 함수를 필요로 한다.
- h1 : 잘못 위치된 타일의 수
- h2 : 잘못 위치된 타일과 goal 위치와의 거리 합 -> 맨해튼 거리

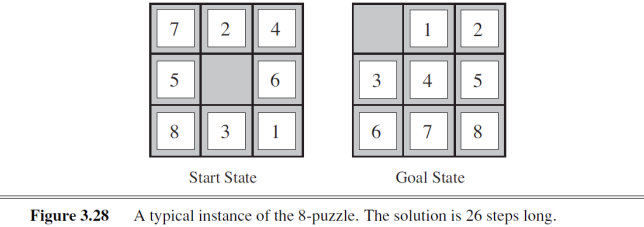
- 위와 같은 상황에서, Start State 의 h1,h2 를 구해보자.
- h1 = 8 (전부 다 잘못된 위치)
- h2 = 3 + 1 + 2 + 2 + 2 + 3 + 3 + 2 = 18
Effect of the Heuristic Accuracy
- A* 의 시간복잡도는 heuristic 의 정확도와 관련이 있다.
- h* 은 정답까지의 실제 비용이며, h 는 추정 비용이다.
- 상대 오차 e 는 다음과 같다.
- e = 0 <= (h* - h) / h* <= 1 , (h* > h)
- 즉, e가 0에 가까울 수록 heuristic 이 정확한 것이다.
- 가장 최적의 알고리즘이였던 IDS 와 A*(h1), A*(h2) 를 비교해보자.
- effective branching factor b*
- d : solution depth
- N + 1 = 1 + b* + (b*)^2 + ... + (b*)^d (N+1 node 개수를 포함하는 식에 b* 가 사용된다.)
- 예로, A* 가 길이 5에서 52개의 node 를 사용해서 solution 을 찾았다면, b* 은 1.92 가 될 것이다.
- 좋은 heuristic 은 b* 가 1에 가까울 것이다.
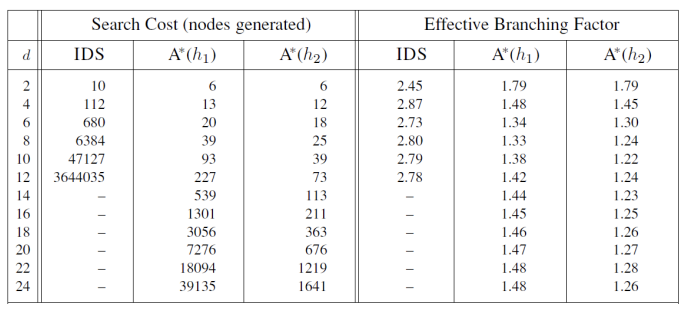
- IDS > A*(h1) > A*(h2) 의 순서대로 비용이 큰 것을 볼 수 있다.
- 또한, effective branching factor b* 도 IDS > A*(h1) > A*(h2) 순으로 크다.
Comparision of Heuristics
- n-puzzle 문제에서 h2 는 언제나 h1 보다 더 좋은 결과를 내놓으며, 이를 h2가 h1 을 dominate (지배) 했다 라고 한다.
- 따라서 h2는 절대 h1 이 expand 한 노드 수보다 많은 수를 expand 할 수 없다.
- 증명은 다음과 같다.
- f(n) < c* 인 모든 노드는 expand 된다. (c* 은 최적의 경로 비용)
- f(n) = g(n) + h(n) < c*
- h(n) < c* - g(n)
- h1 을 사용한 A* 은 h2 를 이용한 A* 가 만들어낸 모든 노드를 포함한다. 그러나 그 역은 성립되지 않는다.
- 왜냐하면 h1(n) <= h2(n) < C* - g(n) 이기 때문이다.
- 항상 h1 <= h2 이다.
(둘다 admissible 하다. h1 은 항상 경로비용보다 작거나 같을 것이고, h2 도 마찬가지다. 왜냐하면 실제 경로에선 가로막힌 타일이 존재하여 goal 까지의 맨해튼 거리 이상의 경로가 나올 수 있기 때문이다.)
- 만약 한 타일이 잘못된 위치라면, h1 에서는 1을 더해줄 것이다. 그러나 h2 에서는 잘못된 타일에서부터 goal 위치까지의 거리를 구해야 하므로 항상 1 이상의 거리 일 것이기 때문이다.
Generating Admissible Heuristics from Relaxed Problems
- n-puzzle 문제에서 사용되었던 h1 와 h2 는 또한 간단하게 변형된 문제에서도 경로 비용이 정확하다.
- 그러한 변형 문제를 Relaxed Problem 이라고 한다.
- h1 : 타일을 뜯고, 아무곳으로 한번에 이동 가능한 타일
- h2 : 빈칸이든 아니든 상관없이 한 칸씩 이동 가능한 타일
Relaxed Problems
- Relaxed 문제는 원래 문제의 state space 에 edge 를 추가한다.
- 여기서 edge 는 action 을 의미한다.
- 원래의 original 문제는 relaxed problem 보다 풀기 어렵기에, 원래 문제의 정답은 당연히 relaxed problem 의 정답이다.
- 그러나 relaxed problem 은 edge가 지름길을 제공한다면 더 좋은 solution 을 가질 수 있다.
- 따라서 relaxed 문제의 optimal solution 은 original 문제의 admissible heuristic 이다.
- 즉, relaxed solution 은 항상 original 의 실제 비용보다 비용이 작다는 것이다. -> admissible heuristic!
- 또한, consistent 하다.
Automatic Construction of Relaxed Problems
- 이를 위해서는 문제 정의를 위한 formal language 가 필요하다.
- n-puzzle 문제의 경우,
- 아래 조건을 만족시킨다면 타일은 위치 A 에서 위치 B로 이동할 수 있다.
- A는 B와 수직 혹은 수평으로 인접해있다.
- B는 빈칸이다.
- 3가지 relaxed problems 가 파생 가능하다.
- B가 빈칸이 아니여도 인접하기만 하면 이동할 수 있다. -> h2
- B가 인접하지 않더라도 빈칸이기만 하면 이동할 수 있다 -> h3
- B가 어떻든간에 무조건 이동할 수 있다 -> h1
- 단, relaxed problem 이 원래 문제의 heuristic 이 되려면, 그 문제가 풀기 어려워선 안된다.
- 왜냐하면 heuristic 으로 쓰려고 푸는 문제가 오래걸린다면, 실용적이지 않기 때문이다.
- 즉, relaxed problem 상의 solution 이 search 없이 빠르게 찾아지는 경우에만 optimal 하다.
'인공지능' 카테고리의 다른 글
| Local Search, Hill-Climbing Search (0) | 2021.10.18 |
|---|---|
| Admissible Heuristics from Subproblems, Pattern Databases (0) | 2021.10.18 |
| Informed search, Greedy Best-first Search, A* Search (0) | 2021.10.17 |
| Iterative Deepening Depth-First Search, Bidirectional Search (0) | 2021.10.17 |
| Depth-First Search, Depth-Limited Search (0) | 2021.10.17 |



댓글