문제
두 개의 문자열 A와 B가 주어졌을 때, 문자열 A를 편집하여 문자열 B로 만들고자 합니다. 문자열 A를 편집할 때는 다음의 세 연산 중에서 한 번에 하나씩 선택하여 이용할 수 있습니다.
- 삽입(Insert) : 특정한 위치에 하나의 문자를 삽입합니다.
- 삭제(Remove) : 특정한 위치에 있는 하나의 문자를 삭제합니다.
- 교체(Replace) : 특정한 위치에 있는 하나의 문자를 다른 문자로 교체합니다.
이때 편집 거리란 문자열 A를 편집하여 문자열 B로 만들기 위해 사용한 연산의 수를 의미합니다. 문자열 A를 문자열
B로 만드는 최소 편집 거리를 계산하는 프로그램을 작성하세요. 예를 들어 "sunday"와 "saturday"의 최소 편집 거리는 3입니다.
입력 조건
- 두 문자열 A와 B가 한 줄에 하나씩 주어집니다.
- 각 문자열은 영문 알파벳으로만 구성되어 있으며, 각 문자열의 길이는 1보다 크거나 같고, 5,000보다 작거나 같습니다.
출력 조건
최소 편집 거리를 출력합니다.
입력 예시 1
cat
cut
출력 예시 1
1
입력 예시 2
sunday
saturday
출력 예시 2
3
나의 풀이
A = input()
B = input()
n = len(A)
m = len(B)
dp = [[0] * (m+1) for _ in range(n+1)]
for i in range(n+1) :
dp[i][0] = i
for j in range(m+1) :
dp[0][j] = j
for i in range(1,n+1) :
for j in range(1,m+1) :
# 문자열이 같다면 왼쪽 위 값과 똑같이
if A[i-1] == B[j-1] :
dp[i][j] = dp[i-1][j-1]
# 문자가 다르다면 왼쪽 위(교체), 왼쪽(삽입), 위쪽(삭제) 중에서 최솟값 찾기
else :
dp[i][j] = 1 + min(dp[i-1][j-1], dp[i][j-1], dp[i-1][j])
print(dp[n][m])dp[] 점화식을 이해하는데 한참이 걸린 문제... 다음에 이런 문제를 만나면 또 풀 수 있을까 싶긴 하지만, 최대한 문제유형에 익숙해지자! 아예 방법을 외워버리는 것도 괜찮을지도?
이 문제는 최소 편집 거리를 담을 2차원 테이블을 만들고, 최소 편집 거리를 계산해 테이블에 저장하며, dp[n][m] 값이 총 최소 편집 거리가 된다.
sunday 와 saturday 를 비교한 최종 2차원 테이블의 결과는 다음과 같다.
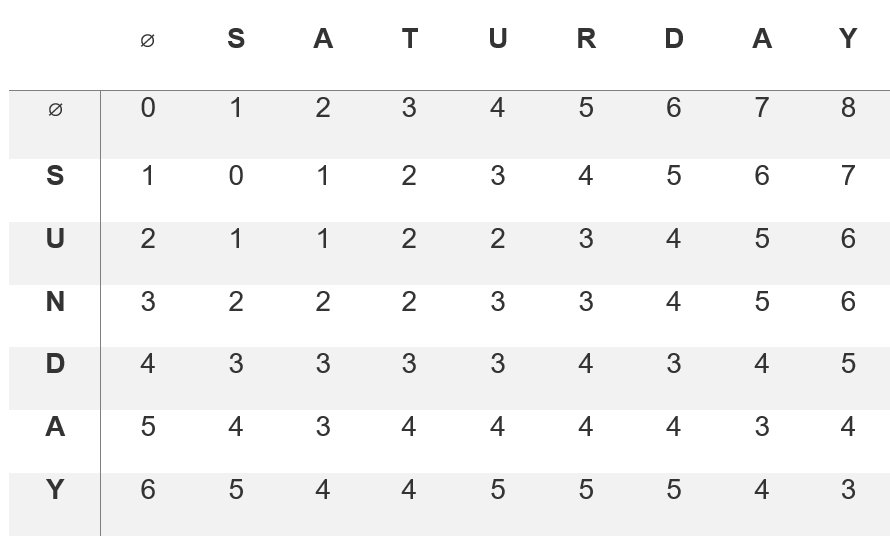
- 두 문자가 같은 경우: dp[i][j] = dp[i-1][j-1]
- 행과 열에 해당하는 문자가 서로 같다면, 왼쪽 위에 해당하는 수를 그대로 삽입
- 두 문자가 다른 경우: dp[i][j] = 1 + min(dp[i][j-1], dp[i-1][j], dp[i-1][j-1])
- 행과 열에 해당하는 문자가 서로 다르다면, 왼쪽(삽입), 위쪽(삭제), 왼쪽 위(교체) 에 해당하는 수 중에서 가장 작은 수에 1을 더해 대입
문자열을 부분으로 잘라 본다면, 더 이해하기 쉬울 것이다.
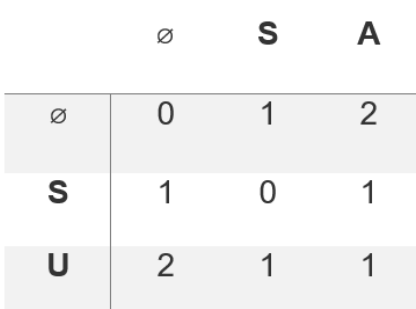
- U와 A를 비교하는 상황에서, 만약 U와 A가 같다면 dp[2][2] = dp[1][1] , 즉 0 이 될 것이다.
- U와 A가 다른 경우엔 왼쪽위/왼쪽/위의 dp중 최솟값을 찾고, 그 dp값에 알맞는 교체/삽입/삭제 연산 횟수 1을 더해주면 된다.
- 삭제/위쪽 dp + 1
- 위쪽으로 옮길 시, SU에서 U는 삭제되고, S와 SA를 비교하는 셈이 된다. 따라서 현재 문자인 U를 삭제하는 연산인 것이다.
- 교체/왼쪽 위 dp + 1
- 왼쪽 위로 옮길 시, SU에서 U도 없어지고, SA에서 A도 없어지는 것이므로 이는 S와 S를 비교하고, 현재문자는 해당문자로 교체하는 연산인 것이다.
- 삽입/왼쪽 dp + 1
- 왼쪽으로 옮길 시, SU는 그대로이고, SA에서 A는 삭제되고 S만 남게된다. 즉, SU 의 입장에서는 비교대상인 위쪽 문자가 한 개 줄어든 것이므로, 삽입연산으로 볼 수 있다.
- 삭제/위쪽 dp + 1
- 위의 경우에는, dp[i-1][j-1]의 값이 최솟값이므로 교체연산이 적절하다고 볼 수 있다.
'알고리즘 > 동적프로그래밍(DP)' 카테고리의 다른 글
| [swea] 3282번: 0/1 Knapsack - 파이썬(python) (0) | 2022.11.12 |
|---|---|
| [swea] 3304번: 최장 공통 부분 수열 - 파이썬(python) (0) | 2022.11.12 |
| [백준] 18353번: 병사 배치하기 - 파이썬(python) (0) | 2022.10.19 |
| [백준] 1932번: 정수 삼각형 - 파이썬(python) (0) | 2022.10.19 |
| [프로그래머스] 사칙연산 - 파이썬(python) (0) | 2022.09.20 |



댓글