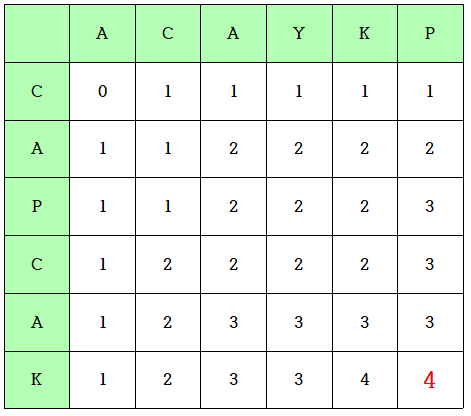
s1 = CAPCAK, s2 = ACAYKP 의 문자열에서 최장 공통부분,
Longest Common Subsequence (LCS) 을 찾자.
dp값을 구하는 방법은 다음과 같다.
if (arr[i] == arr[j]) dp[i][j] = dp[i-1][j-1] + 1;
if (arr[i] != arr[j]) dp[i][j] = max(dp[i][j-1], dp[i-1][j]);- 만약 s1의 i번째 문자열과 s2의 j번째 문자열이 같다면, 이는 dp[i-1][j-1] +1 과 같을 것이다. s1의 i-1번째까지와 s2의 j-1번째까지 비교한 값 + 1 의 값이기 때문이다.
- ex) dp[2][3] 의 경우, dp[1][2] (C와 AC 를 비교한 값 : 1) + 1과 같다.
- 만약 s1의 i번째 문자열과 s2의 j번째 문자열이 다르다면, dp[i-1][j] 까지 구한 것 혹은 dp[i][j-1] 까지 구한 것 중 큰 값이 될 것이다. 즉, s1의 i-1번째까지와 s2 j번째까지 비교한 값 or s2의 i번째까지와 s2의 j-1번째까지 비교한 값 중 큰 값이다.
- ex) dp[2][4] 의 경우, A와 Y가 같지 않기 때문에 dp[2][3] (CA와 ACA를 비교한 값 : 2) or dp[1][4](C와 ACAY를 비교한 값 : 1) 중 큰 값과 같다.
나의 코드
T = int(input())
answer = []
for t in range(1, T + 1):
a, b = input().split()
dp = [[0] * (len(b) + 1) for _ in range(len(a) + 1)]
for i in range(1, len(a)+1):
for j in range(1, len(b)+1):
if a[i - 1] == b[j - 1]:
dp[i][j] = dp[i - 1][j - 1] + 1
else:
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
answer.append(f'#{t} {dp[-1][-1]}')
print(*answer, sep='\n')
이런 유형의 경우, 한 번도 풀어보지 않았다면 dp점화식을 떠올리기가 쉽지 않을 것 같다.
나도 처음엔 DFS 로 접근했다가, 문자열의 길이가 1000이하라 시간초과를 피할 수 없음을 직감하고, dp로 전환하였다.
많은 유형의 문제를 풀어보아야겠다...
'알고리즘 > 동적프로그래밍(DP)' 카테고리의 다른 글
| [백준] 1890번: 점프 - java (0) | 2023.02.02 |
|---|---|
| [swea] 3282번: 0/1 Knapsack - 파이썬(python) (0) | 2022.11.12 |
| [이코테] 편집거리 - 파이썬(python) (0) | 2022.10.20 |
| [백준] 18353번: 병사 배치하기 - 파이썬(python) (0) | 2022.10.19 |
| [백준] 1932번: 정수 삼각형 - 파이썬(python) (0) | 2022.10.19 |



댓글