처음엔 백트래킹으로 문제를 풀었는데, 제한시간 초과로 실패하게 되었다.
백트랙킹의 경우 보통 시간 복잡도가 2^n 에 근접하다.
따라서 n이 20이하인 경우에만 백트래킹을 사용해야 한다.
이 문제의 경우 n=100 이므로, 2^100은 당연히 시간초과를 일으킬 것이다....
따라서 dp를 사용하자!
dp[i][j] 에서 i는 i번째 물건까지 선택할 수 있음을 뜻하고, j는 j무게까지 물건을 담을 수 있음을 뜻한다.
현재 물건무게가 j 보다 크다면, 해당 물건을 선택할 수 없으므로 [이전 물건][같은 무게] (dp[i-1][j]) 를 입력해준다.
현재 물건무게가 j이하라면, 둘 중 더 큰 값을 선택한다.
- 현재 물건을 넣어준다. 현재물건가치 + knapsack[i-1][j-weight] (이전물건, j-현재물건무게) 을 더한다.
- 현재 물건을 선택하지 않는게 더 크다면 이전물건까지의 값 knapsack[i-1][j] 을 가져온다.
knapsack[N][K]는 곧, 배낭의 최대부피가 K무게일 때의 최댓가치값을 가리킨다.
knapsack[i][j] = max(현재 물건 가치 + knapsack[이전 물건][현재 가방 무게 - 현재 물건 무게], knapsack[이전 물건][현재 가방 무게])
knapsack[i][j] = max(value + knapsack[i - 1][j - weight], knapsack[i - 1][j])
출처 : https://gsmesie692.tistory.com/113
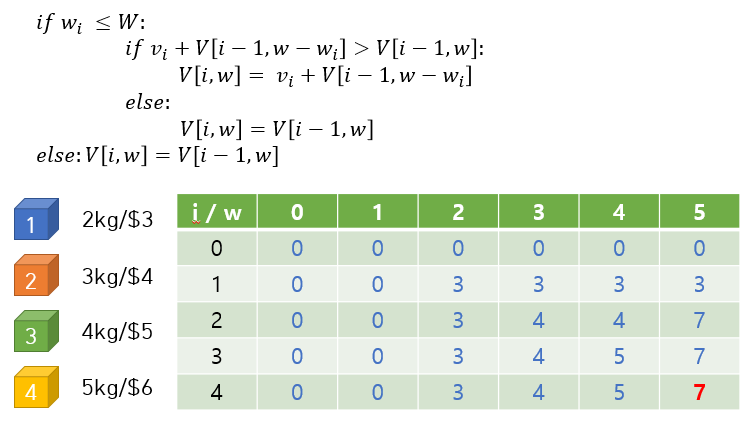
정말 정리가 잘 된 블로그를 통해 이해를 쉽게 할 수 있었다.
특히 그림과 dp 표를 통해 하나하나 직접 시뮬레이션을 해보면 이해가 더 쉬울 것이다.
i=2 이고, 최대무게 w=5 인 상황을 살펴보자.
현재는 2번 가방을 선택할 수 있는 상황이다.
2번 가방의 무게가 3kg 로, 최대무게 (5kg) 이하이므로, 가방을 선택할 수 있다.
따라서 두 가지 선택지 중 골라야 한다.
- 2번 가방을 선택하지 않았을 때의 가치가 더 큰 경우 -> 1번가방까지 선택하고 5가 최대무게인 경우 -> dp[1][5] = 3
- 2번 가방을 선택해야 가치가 더 큰 경우 -> 1번가방까지 선택하고, 5-3 의무게가 최대무게였을 때의 최대가치 + 2번가방의 가치 -> dp[1][2] + 4 = 3+4 = 7
이므로, 2번 가방을 선택하는 경우에 최대 가치를 갱신할 수 있다.
나의 풀이
T = int(input())
answer = []
for t in range(1, T + 1):
n, k = map(int, input().split())
arr = [(0, 0)]
for _ in range(n):
v, c = map(int, input().split())
arr.append((v, c))
# dp[i][j] 에서 i번째 물건까지 고를 때 j무게일 때의 가치 최댓값
dp = [[0 for _ in range(k + 1)] for _ in range(n + 1)]
for i in range(1, n + 1):
for j in range(1, k + 1):
weight, value = arr[i][0], arr[i][1]
if weight > j: # 무게가 j보다 크다면 [이전물건까지][j]
dp[i][j] = dp[i - 1][j]
else:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight] + value)
answer.append(f'#{t} {dp[n][k]}')
print(*answer, sep='\n')'알고리즘 > 동적프로그래밍(DP)' 카테고리의 다른 글
| [백준] 11660번: 구간 합 구하기 5 - java (1) | 2023.02.04 |
|---|---|
| [백준] 1890번: 점프 - java (0) | 2023.02.02 |
| [swea] 3304번: 최장 공통 부분 수열 - 파이썬(python) (0) | 2022.11.12 |
| [이코테] 편집거리 - 파이썬(python) (0) | 2022.10.20 |
| [백준] 18353번: 병사 배치하기 - 파이썬(python) (0) | 2022.10.19 |



댓글